MATERI TREE (POHON)

MATERI TREE (POHON)

v Definisi

·          Pohon (Tree) adalah graf tak-berarah terhubung yang tidak mengandung sirkuit

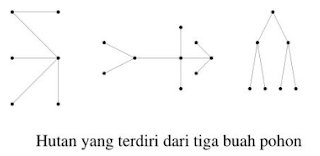
·         Hutan (forest) adalah 

-          kumpulan pohon yang saling lepas, atau 

-          graf tidak terhubung yang tidak mengandung sirkuit. Setiap komponen di dalam graf terhubung tersebut adalah pohon

v Sifat-sifat Pohon

·         Teorema, Misalkan G= (V, E) adalah graf tak-berarah sederhana dan jumlah simpulnya n. Maka, semua pernyataan di bawah ini adalah ekivalen:

·         G adalah pohon.

·         Setiap pasang simpul di dalam Gterhubung dengan lintasan tunggal.

·         G terhubung dan memiliki m = n–1 buah sisi.

·         G tidak mengandung sirkuit dan memiliki m = n–1  buah sisi.

·         G tidak mengandung sirkuit dan penambahan satu sisi pada graf akan membuat hanya satu sirkuit.

·         G terhubung dan semua sisinya adalah jembatan.

·         Teorema di atas dapat dikatakan sebagai definisi lain dari pohon.

v  Terminologi (1)

·    Anak(childatau children) & Orangtua(parent)

·    b, c, dan dadalah anak-anak simpul a, 

·    a adalah orangtua dari anak-anak itu 

·    Lintasan (path) 

·    Lintasan dari ake jadalah a, b, e, j. 

·    Panjang lintasan dari ake jadalah 3. 

·    Saudara kandung (sibling) 

·    fadalah saudara kandung e, 

·    gbukan saudara kandung e, karena orangtua mereka berbeda.

Subgrapgh

v Terminologi (2)

·         Derajat (degree)

-          Derajat sebuah simpul adalah jumlah subgraph (atau jumlah anak) pada simpul tersebut.

-          Deg(a)=3, Deg(b)= 2, Deg(d)= 1 dan Deg(c)= 0.

-          Jadi, derajat yang dimaksudkan di sini adalah derajat-keluar.

-          Derajat maksimum dari semua simpul merupakan derajat pohon itu sendiri. Pohon di samping berderajat 3

·         Daun (leaf)

-          Simpul yang berderajat nol (atau tidak mempunyai anak) disebut daun. Simpul h, i, j, f, c, l, dan madalah daun.

·         Simpul Dalam (internal nodes)

-          Simpul yang mempunyai anak disebut simpul dalam. Simpul b, d, e, g, dan kadalah simpul dalam.

v Terminologi (3) 

·         Aras (level) atau Tingkat

·         Tinggi (height) atau Kedalaman (depth)

·         Aras maksimum dari suatu pohon disebut tinggi atau kedalaman pohon tersebut. Pohon di atas mempunyai tinggi 4

v Pohon Merentang (spanning tree)

·         Pohon merentang dari graf terhubung adalah subgraph merentang yang berupa pohon 

·         Pohon merentang diperoleh dengan memutus  sirkuit di dalam graf\

·         Setiap graf terhubung mempunyai paling sedikit satu buah pohon merentang

·         Graf tak-terhubung dengan kkomponen mempunyai kbuah hutan merentang yang disebut hutan merentang (spanning forest)

v  Pohon Rentang Minimum

·         Graf terhubung-berbobot mungkin mempunyai lebih dari 1 pohon merentang

·         Pohon rentang yang berbobot minimum – dinamakan pohon merentang minimum (minimum spanning tree)

v Algoritma Prim

·         Ambil sisi (edge) dari graph yg berbobot minimum, masukkan ke dalam T

·          Pilih sisi (edge) (i,j) yg berbobot minimum dan bersisisan dengan simpul di T, tetapi (i,j) tidak membentuk cycle di T. tambahkan (i,j) ke dalam T

·         Ulangi prosedur no 2 sebanyak (n-2) kali

§  Pohon merentang yang di hasilkan tidak selalu unik meskipun bobotnya tetap sama

§  Hal ini akan terjadi jika ada beberapa sisi yang akan di pilih berbobot sama

v Algoritma Kruskal

Ø  Langkah-langkah dalam algoritma Kruskal adalah sebagai berikut:

§  Lakukan pengurutan terhadap setiap sisi di graf mulai dari sisi dengan bobot terkecil sampai terbesar.

§  Pilih sisi yang mempunyai bobot minimum yang tidak membentuk sirkuit di pohon. Tambahkan sisi tersebut ke dalam pohon.

§  Ulangi langkah 2 sampai pohon merentang minimum terbentuk, yaitu ketika sisi di dalam pohon merentang minimum berjumlah n-1 (n adalah jumlah simpul di graf).

v Pohon berakar (Rooted Tree) 

·       Pohon yang satu buah simpulnya diperlakukan sebagai akar dan sisi-sisinya diberi arah sehingga menjadi graf berarah

• CONTOH

v Terminologi pada Pohon Berakar

·         Child atau children (Anak) dan parent (orangtua)

·         Path (lintasan)

·         Descendant (Keturunan) dan ancestor (leluhur)

·         Sibling (saudara kandung)

·         Subtree (subpohon)

·         Degree (derajat)

·         Leaf (daun)

·         Internal nodes (simpul dalam)

·         Level (tingkat)

·         Height (tinggi) atau depth (kedalaman)

v Path (lintasan)

Lintasan dari simpul vi ke simpul vk adalah runtunan simpul-simpul v1, v2 ,…, vk sedemikian hingga vi adalah orangtua dari vi+1 untuk 1 <= i <= K.
Panjang lintasan adalah jumlah sisi yang dilalui dalam suatu lintasan, yaitu k – 1.
Pada gambar G1 : 

·         Lintasan dari a ke j adalah a, b, e dan j 

·         Panjang lintasan dari a ke j adalah 3

v Descendant (Keturunan) dan ancestor (leluhur)

x adalah leluhur dari simpul y jika terdapat lintasan dari simpul x ke simpul y di dalam pohon dan keturunan dari simpul x adalah simpul y.
Pada gambar G1 :

·         Simpul b adalah leluhur dari simpul h

·         Simpul h adalah keturunan dari simpul b

v Sibling (saudara kandung)

Sibling atau saudara kandung adalah simpul yang berorangtua sama
Pada gambar G1 :

·         Simpul f saudara kandung dari e

·         Simpul g bukan saudara kandung dari e karena orangtua berbeda

v Subtree (subpohon) 

Subtree dengan x sebagai akarnya adalah subgraf T’ = (V’,E’) sedemikian hingga V’ mengandung x dan semua keturunannya dan E’ mengandung sisi-sisi dalam semua lintasan yang berasal dari x
Pada gambar G2 :

·         V’ = {b, e, f, h, i, j} 

·         E’ = {(b, e), (b, f), (e, h), (e, i), (e, j)}

·         b adalah simpul akar 

v Degree (derajat) 

Derajat sebuah simpul pohon berakar adalah jumlah subtree (jumlah anak) pada simpul tersebut. Derajat pohon berakar merupakan derajat keluar
Pada gambar G1 :

·         Derajat simpul a : 3, simpul b : 2, simpul c : 0 dan simpul d : 1

·         Derajat tertinggi (maksimum) : 3 

v Leaf (daun)

Adalah simpul yang berderajat nol (tidak mempunyai anak)

Pada gambar G1 :

·         Merupakan daun : simpul c, f, h, i, j, l dan m.

v Internal nodes (simpul dalam) 

Adalah simpul yang mempunyai anak

Pada gambar di samping :

·         Merupakan simpul dalam : simpul b, d, e, g dan k

v Level (tingkat) 

Akar mempunyai level = 0
Level simpul lainnya = 1 + panjang lintasan dari akar ke simpul tersebut (gambar G3).

v Height (tinggi) atau depth (kedalaman)

Adalah level maksimum dari suatu pohon
Nama lain : panjang maksimum lintasan dari akar ke daun
Pada gambar di samping :

·         Pohon mempunyai tinggi atau kedalaman : 4

v Pohon n-ary

·         pohon berakar yang setiap simpul cabangnya mempunyai paling banyak n buah anak.

·         Pohon n-ary dikatakan pohon penuh (full) atau pohon teratur jika setiap simpul cabangnya mempunyai tepat m buah anak.

v Pohon Biner (Binary Tree)

·         Adalah pohon n-ary dengan n=2

·         Pohon yang paling penting karena banyak aplikasinya

·         Setiap simpul di dalam pohon biner mempunyai paling banyak 2 buah anak

·         Di bedakan antara anak kiri (left child) dan anak kanan (right child)

·         Karena ada perbedaan urutan anak, maka pohon biner adalah pohon terurut